GSOC 2017 - Week 2 of GSoC 17

This blog is dedicated to the second week of Google Summer of Code (i.e June 8 - June 15). The target of the second week according to my timeline was to implement the Jacobian and gradient using numdifftools.

Derivative

The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point.

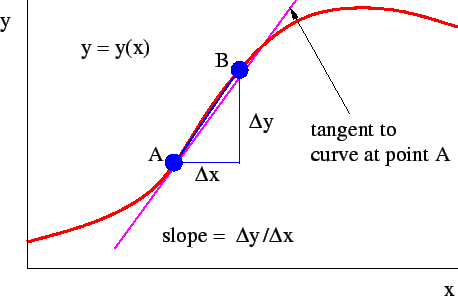
It is derived numerically as :

Gradient

Gradient is a multi-variable generalization of the derivative. While a derivative can be defined on functions of a single variable, for functions of several variables, the gradient takes its place. The gradient is a vector-valued function, as opposed to a derivative, which is scalar-valued. If f(x1, …, xn) is a differentiable, real-valued function of several variables, its gradient is the vector whose components are the n partial derivatives of f.

In 3D gradient can be given as:

Jacobian

The Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. Given as:

Status of Week 2:

• Derivative :

  The code to the derivative can be found here. The code accepts a univariate scalar function and points at which the derivative needs to computed along with a dictionary for options related to step generation, order of derivative and order of error terms as an input. It returns a 1D array of derivative at respective points. The method uses extrapolation and adaptive steps for derivative computation which leads to more accuracy as compared to statsmodels.

  Example:

   Input : derivative((lambda x: x**2), [1,2])
     
   Output : [2,4]
  

• Jacobian :

  The code to the Jacobian can be found here.

  The code accepts a function which can be multivariate and vector as well, vectors (in the form of 2D array) for Jacobian computation a dictionary for options related to step generation, order of derivative and order of error terms as an input. It returns a 2D array for scalar functions and 3D array for vector functions. Each row in the 3D array respresents the jacobian of each vector.

  Example:

  Input : jacobian(lambda x: [[x[0]*x[1]**2], [x[0]*x[1]]], [[1,2],[3,4]])
    
  Output : [array([[ 4.,  4.],[ 2.,  1.]]), array([[ 16.,  24.],[  4.,   3.]])]
  

• Gradient :

  Gradient is considered to be a special case of Jacobian and thus, Gradient returns the value computed by Jacobian.

Next Week’s Target:

• Hessian Implementation using statsmodels and numdifftools.
• Analysis about the accuracy of the functions that are already implemented.

References:

• https://en.wikipedia.org/wiki/Derivative
• https://en.wikipedia.org/wiki/Gradient
• https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant
• https://github.com/pbrod/numdifftools/tree/master/numdifftools