GSOC 2017 - Week 3 of GSoC 17

This blog is dedicated to the third week of Google Summer of Code (i.e June 16 - June 23). But first, a brief insight is given about how the code works.

Step Generators

For computing the derivatives, steps are required with which the apprxoimation is made. Each element in the step generators represent h in .

Choosing the steps are important for approximation. If the steps are very small, derivative becomes inaccurate due to rounding error caused by subtraction. While if steps are too large, the results will be inaccurate due to fomrula error.

The below figure shows the deviations from the null error as the steps are increased or decreased to an extent.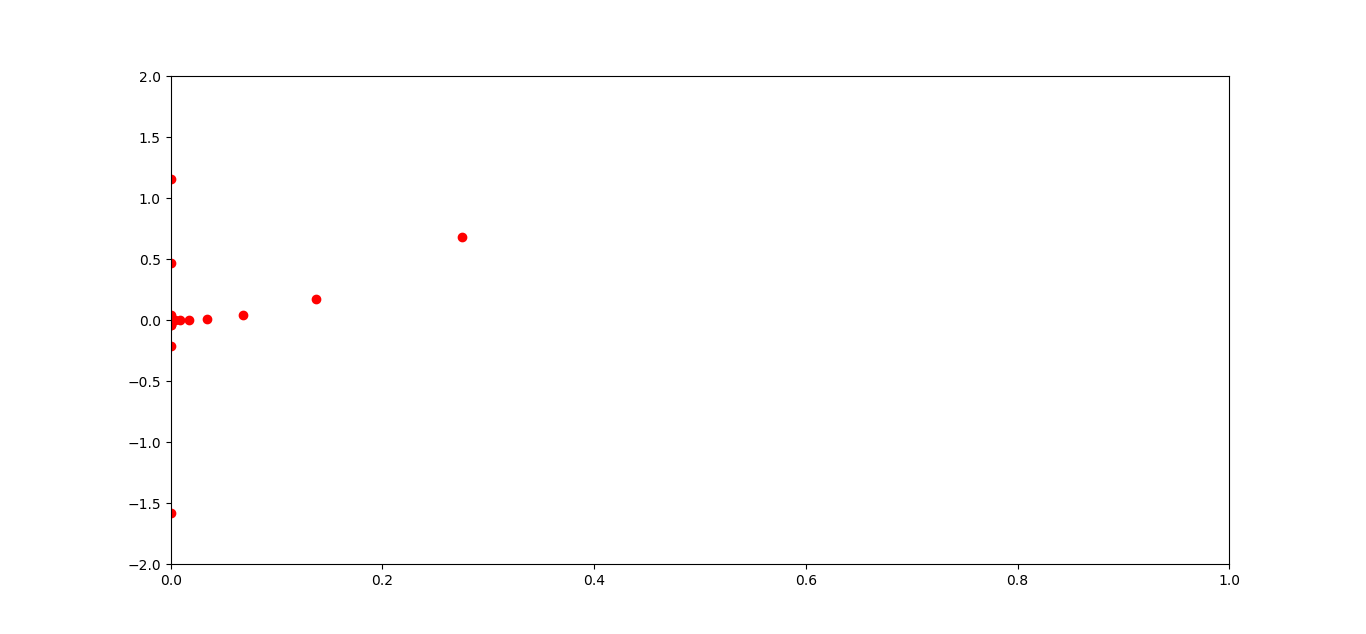

‘max_steps’ generates a decreasing sequence while ‘min_steps’ generates increasing sequence.

For ‘max_steps’: steps are calculated as:

for i in range(num_steps):
        steps = base_step * step_ratio**(-i + offset)
        if (np.abs(steps) > 0).all():
            yield steps

And for ‘min_steps’:

for i in range(num_steps):
        steps = base_step * step_ratio**(i + offset)
        if (np.abs(steps) > 0).all())
            yield steps

where base_step = base_step * step_nom.

### Parameters

• x : array, optional, default is np.asarray(1)

  The points at which steps are to be generated.
  

• n : int, optional, default is 1

  order of derivative.
  

• order : int, optional, default is 2

  defines the order of the error term in the Taylor approximation used.
  

• method : {‘central’, ‘forward’, ‘backward’}, optional, default: ‘central’

  defines the method to be used.
  

• base_step : float, array-like, optional

  Defines the start step.
      
  Default: 2 for max_step,
      
           EPS**(1./scale) for min_step.
  

• scale : real scalar, optional, default is 2.5

  scale used in base step.
  

• num_steps : scalar integer, optional, default 15

  defines number of steps generated.
  

• step_nom : array-like, default maximum(log(1+abs(x)), 1)

  Nominal step is the same shape as x.
  

• step_ratio : real scalar, optional, default 2

  Ratio between sequential steps generated.
      
  If None then step_ratio is 2 for n=1
      
  otherwise step_ratio is 1.6.
  

• offset : real scalar, optional, default 0

  offset to the base step.
  

• step : {‘max_step’, ‘min_step’}, optional, defult ‘max_step’

  Defines the nature of the steps to be generated, increasing or decreasing.
  

Returns

steps : generator

        generator of sequence.

Examples

>>> step_gen = _generate_step(base_step=0.25, step_ratio=2,
                                    num_steps=4, step='min_step')
>>> [s for s in step_gen()]
    [0.25, 0.5, 1.0, 2.0]

Extrapolation

The steps thus generated with fixed step_ratio is then used to calculate the derivative with different h in the finite difference formula. In this manner we use extrapolation to get the correct answer.

Now these calculated derivatives needs to be analysed for least error estimation. Hence, the derivatives are convolved with appropriate coefficients to estimate the result. This method is also a part of Richardson Extrapolation. After convolution, errors are computed by subtracting adjacent values in the array of derivatives.

Then the median of errors are used to statiscally obtain the derivative with least error. Hence, statistical methods like percentile is used to obtain the majority of derivatives in a certain range.

This whole method can be found here.

Hessian

Hessian is a square matrix of second-order partial derivatives of a scalar-valued function.

Status of Week 3:

The Hessian code can be found here :

numdifftools (hessdiag also present) here statsmodels here

Input for Hessian is a univariate/multivariate function returning a scalar value, a 2d array of points at which hessian is to e calculated and other options for step generation. It returns hessian matrix : a 3d array with each row representing the hessian matrix corresponding to each input vector.

Example:

  >>> hessian(lambda x : x[0] + x[1]**2 + x[2]**3, [[1,1,1],[2,2,2]])
    [[[  0.00000000e+00   0.00000000e+00   0.00000000e+00]
      [  0.00000000e+00   2.00000000e+00   0.00000000e+00]
      [  0.00000000e+00   0.00000000e+00   6.00000000e+00]]

     [[  0.00000000e+00   0.00000000e+00   0.00000000e+00]
      [  0.00000000e+00   2.00000000e+00   2.64678414e-16]
      [  0.00000000e+00   2.64678414e-16   1.20000000e+01]]]